Manacher算法

在计算机科学中，最长回文子串或最长对称因子问题是在一个字符串中查找一个最长的连续的回文的子串，例如“banana”最长回文子串是“anana”。最长回文子串并不一定是唯一的，比如“abracadabra”，没有超过3的回文子串，但是有两个回文字串长度都是3：“ada”和“aca”。在一些应用中，我们求出全部的极大回文子串（不被其他回文串包含的回文子串）。

一、算法由来

Manacher于[1]发现了一种线性时间算法，可以在列出给定字符串中从任意位置开始的所有回文子串。并且，Apostolico, Breslauer & Galil [2]发现，同样的算法也可以在任意位置查找全部极大回文子串，并且时间复杂度是线性的。因此，他们提供了一种时间复杂度为线性的最长回文子串解法。另外，Jeuring (1994)[3], Gusfield (1997)[4]发现了基于后缀树的算法。也存在已知的高效并行算法。

在不使用Manacher算法的情况下，使用暴力方法对每一个字符进行向外扩的操作（中心扩展法），直到遇到不匹配的字符就停下来，继续查看下一个字符串，Mancher算法则是基于中心扩展法的基础之上，对扩出来的信息进行处理，这里是 Manacher 算法的精髓。

二、算法思想

Manacher核心步骤有三步:

处理字符串奇偶数之间的差异，统一都变为奇数字符串。
是否有通过中心扩展法记录的最大边界直接能够得到当前字符串的最大回文字符串（加速扩过程）。
进行中心扩展法。

处理字符串奇偶数之间的差异

如果不处理字符串的奇偶之间的差异会怎么样？

我们举个例子ababa这是一个奇数，我们通过中心扩展法，向外不断扩展，直到找到不匹配的位置。在 0 位置的时候我们无法向外扩展因此直接得到 s[0] 的位置最远能扩 0 个位置。在 1 位置的时候，由字符串 b向外扩展，s[0] a 和 s[2] a 相等，得到 s[1] 位置最远能扩 1 个位置。在 2 位置的时候，由字符串 b向外扩展，s[1] b 和 s[3] b 相等，s[0] a 和 s[4] a 相等，得到 s[2] 位置最远能扩 2 个位置。s[3]的情况和s[1]相同，s[4]的情况和s[0]相同，因此ababa最大回文字符串为ababa。

我们再来举一个偶数的例子 abba。在 0 位置的时候我们无法向外扩展因此直接得到 s[0] 的位置最远能扩 0 个位置。在 1 位置的时候我们无法向外扩展因此直接得到 s[1] 的位置最远能扩 0 个位置。在 2 位置的时候我们无法向外扩展因此直接得到 s[2] 的位置最远能扩 0 个位置。在 3 位置的时候我们无法向外扩展因此直接得到 s[3] 的位置最远能扩 0 个位置。实际上我们这个字符串的最大回文字符串是abba!因此我们需要做奇偶处理。

怎么进行做奇偶处理？

在字符串的开头，中间，结尾插入特殊标记符#，用任何不常用的字符都可以，并不会影响结果。例如字符串abba进行处理之后，为#a#b#b#a#。

func manacherSring(s string) []rune {
	runes := []rune(s)
	res := make([]rune, len(s)*2+1)
	for index, i := 0, 0; i < len(res); i++ {
		if (i & 1) == 0 {
			res[i] = '#'
		} else {
			res[i] = runes[index]
			index++
		}
	}
	return res
}

加速扩过程

加速扩过程，我们需要记录三个变量。

维护一个数组 pArr,该数组维护了一个当前字符串所能扩的最大位置。例如#a#b#a#b#a#对应的 pArr 数组为 {1,2,1,4,1,6,1,4,1,2,1}
维护一个 pR 变量，这个变量记录当前扩展能扩展到最远地方，例如#a#b#a#b#a#，在没有遍历之前初始值为 -1，当 s[0] 时，#的最长回文半径为1,最多向外扩展0个位置，因此 pR 为1。当 s[1] 时，a的最长回文半径为2,最多向外扩展2个位置，因此 pR 为3。当 s[2] 时，#的最长回文半径为1,最多向外扩展0个位置，因此 pR 为3,pR不必之前的大,保持不变。当 s[3] 时，b的最长回文半径为4,最多向外扩展3个位置，因此 pR 为7。当 s[4] 时，#的最长回文半径为1,最多向外扩展0个位置，因此 pR 为5,pR比之前的小,保持不变。当 s[5] 时，a的最长回文半径为6,最多向外扩展5个位置，因此 pR 为11,此时已经到达整个字符数组的结尾，所以之后的过程中pR将不再变化。当 s[7] 时，#的最长回文半径为1,最多向外扩展0个位置，因此 pR 为8,pR比之前的小,保持不变。当 s[8] 时，b的最长回文半径为4,最多向外扩展3个位置，因此 pR 为8,pR比之前的小,保持不变。当 s[9] 时，#的最长回文半径为1,最多向外扩展0个位置，因此 pR 为10,pR比之前的小,保持不变。当 s[10] 时，a的最长回文半径为2,最多向外扩展1个位置，因此 pR 为11,pR不必之前的大,保持不变。
整数index。这个变量表示最近一次更新pR时（pR只会在有更大的pR时才会更新），可以说index就是当前能扩到最有边界的回文中心。

如何用这三个变量进行扩过程呢？

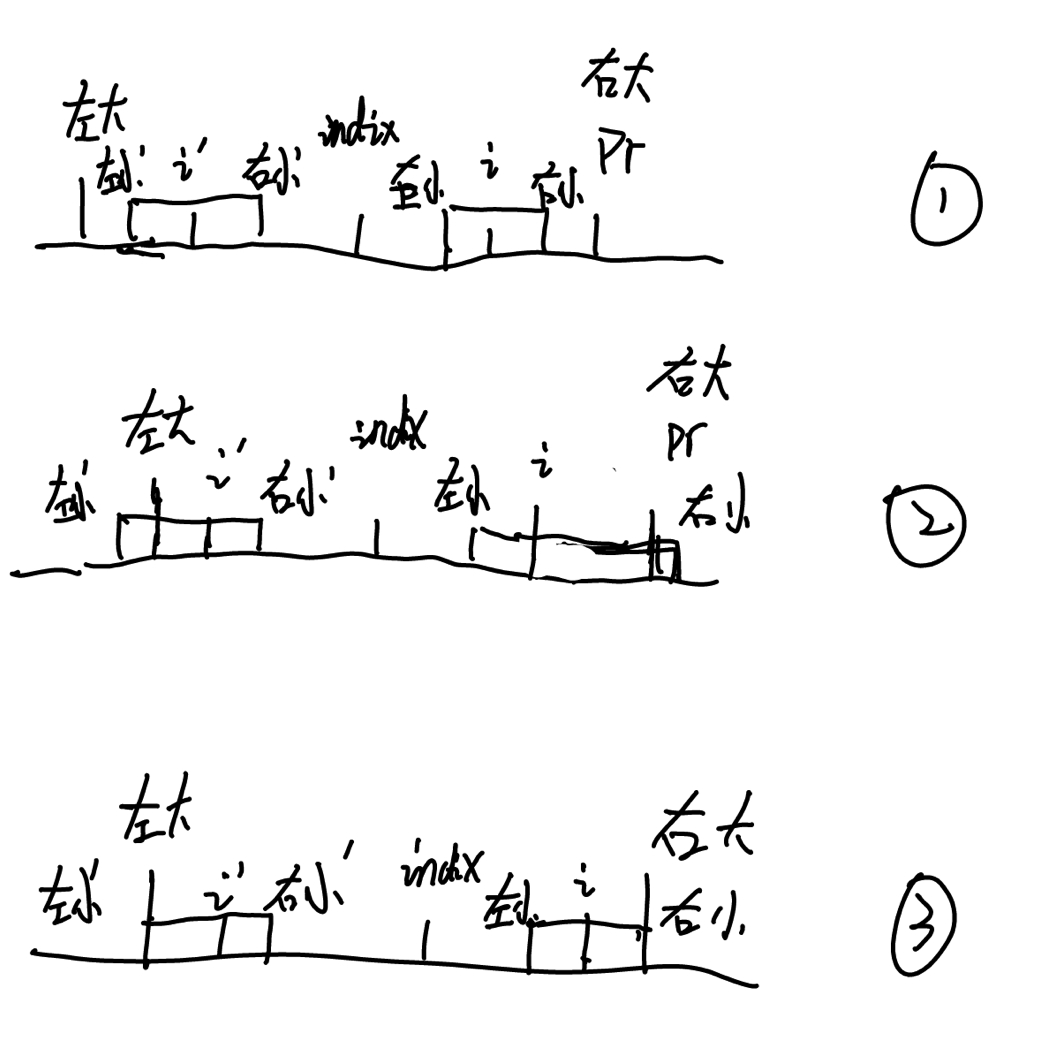
index 是当前包括i的最大扩展的中心位置，其边界我们叫做左大和右大，i 是当前要扩展的位置，因为 i 在扩展中心内，index是一个大回文字符串，那么 i 的回文字符串也应该有 i’ 镜像的回文字符串。在情况 1 下，以 i 为中心的回文字符串被完全包括在大字符串内，那么 i 的扩展到最大的位置一定是 i 的右小边界，不可能超过右小边界，因为 i 字符串完全以 index 为中心扩展，如果可以再向右扩，镜像 i’ 早就应该扩了。在情况 2 下， i 的镜像 i’ 的左小’超过了左大边界，i的字符串最多能扩到右大边界，因为 i 以 index 为镜像，如果 i 能扩到超出右大的边界，同时 i‘ 镜像和 i 的字符串是回文的，index 为什么不继续向外扩展了，因为当前能扩展的最大最位置为右大，因此 i 必定不能向外扩展，i能扩展到的最大值为右大位置。情况下，i’ 的镜像左小‘ 和左大重叠的时候，这个时候 i 以右大为边界可能可以继续向外扩展，这种情况是左小‘的左边一个字符不等于右小’的右边一个字符，整个index字符串没有向外扩，说明左大左边一个字符不等于右大右边一个字符，但是因为右小没有超过右大，左小左边的字符串是有可能等于右小右边的字符串，向外扩展的情况是未知的。

进行中心扩展法

进行处理之后，我们就可以进行扩展

三、算法实现

func maxLcpsLength(s string) int {
	if s == "" {
		return 0
	}
	runes := manacherSring(s)
	pArr := make([]int, 0, len(runes))
	var index, pR, max = -1, -1, math.MinInt32
	for i := 0; i < len(runes); i++ {
		pArr[i] = 1
		if pR > i {
			pArr[i] = pArr[2*index-i]
			if pArr[2*index-i] > pR-i {
				pArr[i] = pR - i
			}
		}
		for ; i+pArr[i] < len(runes) && i-pArr[i] > -1 && runes[i+pArr[i]] == runes[i-pArr[i]]; pArr[i]++ {
		}
		if i+pArr[i] > pR {
			pR = i + pArr[i]
			index = i
		}
		max = int(math.Max(float64(max), float64(pArr[i])))
	}
	return max-1
}