二叉树遍历的方法有很多,例如:前序遍历,中序遍历,后序遍历。但是时间复杂度却只能做到 O(N), 空间时间复杂度 O(N)。今天要介绍是 morris 遍历,时间复杂度可以做到 O(N),空间时间复杂度可以做到 O(1)。
一、Morris 遍历 1. 该算法是如何做到空间时间复杂度为 O(1) 在我们之前学习过的算法中,遍历二叉树的算法都会使用到栈空间,假如不递归,也会使用栈结构,所以空间时间复杂度是 O(N)无法避免。而 Morris 遍历则是使用当前节点的左节点的最右节点指向当前节点,来保证可以回到上层,所以不用使用栈空间结构。
2. 算法流程
从根节点开始遍历
首先看左节点是否为空
如果为空
否则直接遍历右节点
如果左节点不为空,则找到左节点的最右节点
如果最右节点指向的是当前节点,则将其置为空
如果最右节点指向的是空,那么就将最右节点指向当前节点,直接进入下一次循环,从步骤 1
向右遍历
3. Morris 遍历是如何遍历完下层,然后回到上一层 在之前说的算法流程中提过,将当前左节点的最右指针指向,这一次是第一次遍历到这个位置,当遍历到下层的时候,没有最左节点的时候,就会顺着我们定义好的右节点指向上一层节点移动,这个时候就回到了上层,然后往右遍历,会遍历到最右节点第二次。所以该节点会被遍历到两次。
二、 代码实现 morris 遍历 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def morris (node: TreeNode) : cur = node while cur is not None : mostRight: TreeNode = cur.left if mostRight is not None : while mostRight.right is not None and mostRight.right is not cur: mostRight = mostRight.right if mostRight.right is None : mostRight.right = cur cur = cur.left continue else : mostRight.right = None else pass cur = cur.right
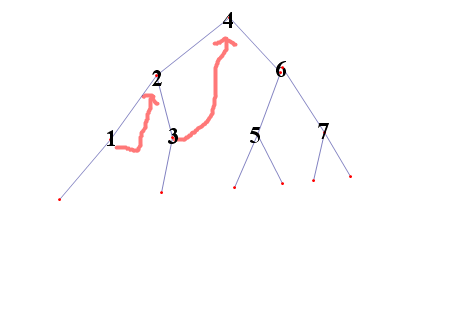
和我说算法流程一样,我就不解释了。解释一下遍历的位置,1 位置遍历到是每一个节点的起始节点,可以说是父母节点,2 位置则是第二次遍历的位置,此时子节点已经遍历完毕,该位置为后根节点 ,3 位置可以说是右节点的遍历。
根据 morris 遍历,我们可以加工出前序遍历,中序遍历,后序遍历。
前序遍历 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def preMorris (node: TreeNode, f) : cur = node while cur is not None : mostRight: TreeNode = cur.left if mostRight is not None : while mostRight.right is not None and mostRight.right is not cur: mostRight = mostRight.right if mostRight.right is None : mostRight.right = cur f(cur.val) cur = cur.left continue else : mostRight.right = None else : f(cur.val) cur = cur.right
根据我一开始的解释,应该能看的很明白,先遍历先根节点(包括左节点),后遍历右节点。
中序遍历 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 def orderMorris (node: TreeNode, f) : cur = node while cur is not None : mostRight: TreeNode = cur.left if mostRight is not None : while mostRight.right is not None and mostRight.right is not cur: mostRight = mostRight.right if mostRight.right is None : mostRight.right = cur cur = cur.left continue else : mostRight.right = None else : pass f(cur.val) cur = cur.right
中序遍历可以直接使用最外面一层,最外一层的遍历方式就是,查找到最左节点后,这个时候才会走到中序遍历的过程,这个时候遍历的就是最左节点,然后最左节点的右节点指向上一层节点(父母节点),也就是根节点,然后根节点,首先会将mostRight.right置为空,然后执行cur = cur.right往右遍历。此时遍历到的节点就是左根右,符合中序遍历,然后递推到整个过程就会将整棵树遍历完。
后序遍历 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 def reverseEdge (mostRight) -> TreeNode: pre = None while mostRight is not None : next = mostRight.right mostRight.right = pre pre = mostRight mostRight = next return pre def printEdge (mostRight, f) : head: TreeNode = reverseEdge(mostRight) while head is not None : f(head.val) reverseEdge(head) def postmorris (node: TreeNode, f) : cur = node while cur is not None : mostRight: TreeNode = cur.left if mostRight is not None : while mostRight.right is not None and mostRight.right is not cur: mostRight = mostRight.right if mostRight.right is None : mostRight.right = cur cur = cur.left continue else : printEdge(mostRight, f) mostRight.right = None cur = cur.right printEdge(node, f)
后序遍历会稍微复杂点,其只用用到了第二次遍历,这个时候已经遍历到最左位置,过程为翻转最右链表,然后遍历,翻转回来,那么得到的结果就是左节点先被遍历到,然后是右节点,然后遍历到上一层后的节点就是根节点,那么顺序就是左右根。翻转第一次为了得到后序遍历顺序,翻转第二次,防止破坏原来的数据结构。遍历到最后只有head节点的右链表,因为head节点没有上层节点,所以head永远都不会进入 1 和 2 。所以最后我们需要手动遍历head节点。
三、总结 morris 遍历作为一种不错的优化手段,其后序遍历较为复杂外,前序遍历和中序遍历都很简单,在这两种遍历的情况下,可以优先选择这种遍历。后序遍历的话,对空间复杂度有要求的话,则可以使用。当然其实都可以在日常使用这种遍历方式去遍历二叉树,因为也都不是很复杂。