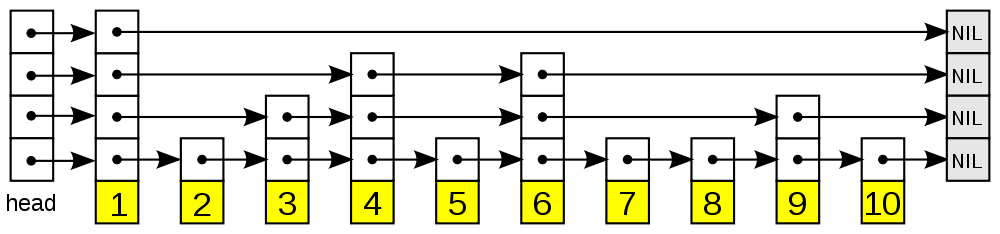
跳跃列表是一种数据结构。它允许快速查询一个有序连续元素的数据链表。跳跃列表的平均查找和插入时间复杂度都是O(log n),优于普通队列的O(n)。
白话跳跃表 我们知道如果是普通的链表,查找为O(n),插入也会O(n),如果是数据量过大的情况下,肯定是无法忍受的,怎么办?给链表加索引,比如说给100个数里面随机给10个数加索引,如果索引分布均匀的话,那么时间复杂是不是最多查找11次?,如果11次还嫌长了怎么办?继续提升索引,提升索引这个比例我们设置为50%,这样可以保证索引在每一层都能分布均匀,且上一层的索引数,差不多是下一层的两倍。听我这样讲是不是感觉很像平衡树的样子,是不是过程看起来很像。
跳跃表和平衡树的区别 跳跃列表不像平衡树等数据结构那样提供对最坏情况的性能保证:由于用来建造跳跃列表采用随机选取元素进入更高层的方法,在小概率情况下会生成一个不平衡的跳跃列表(最坏情况例如最底层仅有一个元素进入了更高层,此时跳跃列表的查找与普通列表一致)。但是在实际中它通常工作良好,随机化平衡方案也比平衡二叉查找树等数据结构中使用的确定性平衡方案容易实现。跳跃列表在并行计算中也很有用:插入可以在跳跃列表不同的部分并行地进行,而不用对数据结构进行全局的重新平衡。
跳跃表实现原理
从上面skiplist的创建和插入过程可以看出,每一个节点的层数(level)是随机出来的,而且新插入一个节点不会影响其它节点的层数。因此,插入操作只需要修改插入节点前后的指针,而不需要对很多节点都进行调整。这就降低了插入操作的复杂度。实际上,这是skiplist的一个很重要的特性,这让它在插入性能上明显优于平衡树
代码实现 下面我粘贴的是维基百科的伪代码实现,具体实现过程和伪代码差不多,提升节点采用是50%概率提升,来保证跳表索引高度为 log n。
伪代码如下 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 make all nodes level 1 j ← 1 while the number of nodes at level j > 1 do for each i'th node at level j do if i is odd if i is not the last node at level j randomly choose whether to promote it to level j+1 else do not promote end if else if i is even and node i-1 was not promoted promote it to level j+1 end if repeat j ← j + 1 repeat
使用 golang 实现跳跃表 node 节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 package jumptabletype Node struct { key int value interface {} up, down, left, right *Node level int } func newNode (k int , v interface {}) *Node return &Node{ key: k, value: v, } } func (n *Node) equals (node *Node) bool if node == nil { return false } if n.key != node.key { return false } if n.value != node.value { return false } if n.level != node.level { return false } return true }
跳跃表
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 package jumptableimport ( "math/rand" "time" ) type jumpTable struct { header *Node r *rand.Rand } func New () *jumpTable return &jumpTable{ r: rand.New(rand.NewSource(time.Now().UnixNano())), header: newNode(-int (^uint (0 ) >> 1 ), nil ), } } func (jt *jumpTable) Search (k int ) *Node println ("walkPreviousNode" ) node, count := walkPreviousNode(jt.header, k) println ("共需要" , count, "步" ) return node } func (jt *jumpTable) Insert (k int , v interface {}) sn := jt.header newN := newNode(k, v) node, _ := walkPreviousNode(sn, k) if node.key == k { node.value = v return } currentLevel := 0 newN.level = currentLevel jt.setNode(newN, node) lowNode := newN for jt.isPromotion() { println ("isPromotion" ) currentLevel++ upNewN := setUpNewDownNode(currentLevel, k, v, newN) if jt.header.level < currentLevel { updateHeader(jt, upNewN) } leftUpNode := findLeftUpNode(lowNode, upNewN) if leftUpNode != nil { jt.setNode(upNewN, leftUpNode) } newN = upNewN } } func updateHeader (jt *jumpTable, upNew *Node) jt.header = upNew } func setUpNewDownNode (level int , k int , v interface {}, newN *Node) *Node upNew := newNode(k, v) upNew.level = level newN.up = upNew upNew.down = newN return upNew } func findLeftUpNode (newN *Node, upNew *Node) *Node var leftUpNode *Node leftNewNode := newN.left leftBreak: for leftNewNode != nil { leftNewUpNode := leftNewNode.up for leftNewUpNode != nil { if leftNewUpNode.level == upNew.level { leftUpNode = leftNewUpNode break leftBreak } leftNewUpNode = leftNewUpNode.up } leftNewNode = leftNewNode.left } return leftUpNode } func (jt *jumpTable) setNode (q *Node, p *Node) q.left = p if p.right != nil { q.right = p.right p.right.left = q } p.right = q } func walkPreviousNode (curNode *Node, k int ) (*Node, int ) println ("k:" , k, " level" , curNode.level) count := 0 for curNode.key < k { count++ if curNode.right == nil { break } println ("curNode.key < k " , curNode.key, "-->" , curNode.right.key) curNode = curNode.right } for curNode.key > k { count++ if curNode.left == nil { break } println ("curNode.key > k " , curNode.key, "-->" , curNode.left.key) curNode = curNode.left } if curNode.down != nil { var newCount int println ("curNode.down " , curNode.key, "-->" , curNode.down.key) curNode, newCount = walkPreviousNode(curNode.down, k) count += newCount } return curNode, count } func (jt *jumpTable) isPromotion () bool n := jt.r.Intn(2 ) if n == 0 { return false } return true }
进行测试
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 package jumptableimport ( "math/rand" "testing" "time" ) func TestJumpTable_Insert (t *testing.T) for i:=0 ;i <1 ;i++ { table := New() r := rand.New(rand.NewSource(time.Now().UnixNano())) table.Insert(13 , nil ) for i := 0 ; i < 1000 ; i++ { table.Insert(r.Intn(100000 ), nil ) } node := table.Search(13 ) if node.key != 13 { panic ("" ) } println (node.key) } }
walkPreviousNode
k: 13 level 12
curNode.down 18542 --> 18542
k: 13 level 11
curNode.down 18542 --> 18542
k: 13 level 10
curNode.down 18542 --> 18542
k: 13 level 9
curNode.down 18542 --> 18542
k: 13 level 8
curNode.key > k 18542 --> 2659
curNode.down 2659 --> 2659
k: 13 level 7
curNode.down 2659 --> 2659
k: 13 level 6
curNode.down 2659 --> 2659
k: 13 level 5
curNode.down 2659 --> 2659
k: 13 level 4
curNode.down 2659 --> 2659
k: 13 level 3
curNode.key > k 2659 --> 1626
curNode.down 1626 --> 1626
k: 13 level 2
curNode.down 1626 --> 1626
k: 13 level 1
curNode.key > k 1626 --> 1436
curNode.down 1436 --> 1436
k: 13 level 0
curNode.key > k 1436 --> 1270
curNode.key > k 1270 --> 996
curNode.key > k 996 --> 964
curNode.key > k 964 --> 957
curNode.key > k 957 --> 848
curNode.key > k 848 --> 792
curNode.key > k 792 --> 759
curNode.key > k 759 --> 671
curNode.key > k 671 --> 513
curNode.key > k 513 --> 413
curNode.key > k 413 --> 99
curNode.key > k 99 --> 28
curNode.key > k 28 --> 13
共需要 28 步
13
可以看见差不多时间复杂度是O(log n)
总结 作为一种简单的数据结构,在大多数应用中Skip lists能够代替平衡树。Skiplists算法非常容易实现、扩展和修改。Skip lists和进行过优化的平衡树有着同样高的性能,Skip lists的性能远远超过未经优化的平衡二叉树。